Project: Multi-Modal Optimization In Surtrac
Keywords: ML algorithms, generalized predictive models, scientific computing, resource allocation, distributed simulations
Goal: Active management of transit vehicles (e.g., buses) in Surtrac
Problems:
- Transit vehicle flow patterns differ significantly from regular cars
- This is due to frequent stops and uncertain dwell times
- This causes significant traffic flow disruptions, increased wait & delay times
Solutions:
- Develop ML-predictive algorithms to accurately estimate dwell times
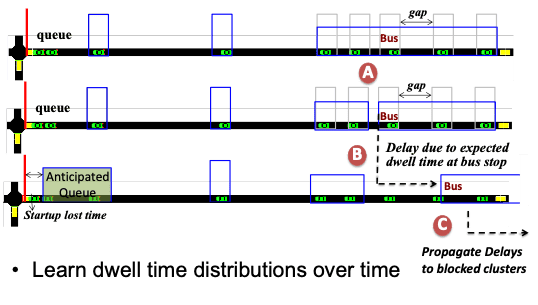
- Extend the flow model in Surtrac to incorporate this information
- Weight clusters by mode type to give priority
Stage-I: Analyze Statistical Trends In DT
Data
- Data – 2+ years of Port Authority data on buses moving along the Centre Avenue corridor (> 3M data points)
- For each data point: stop id, day of week, direction, arrival times, departure times, miles (minutes) from last stop, load, number of passengers on (off), etc.
Findings
- There is strong seasonal correspondence of dwell times from year to year.
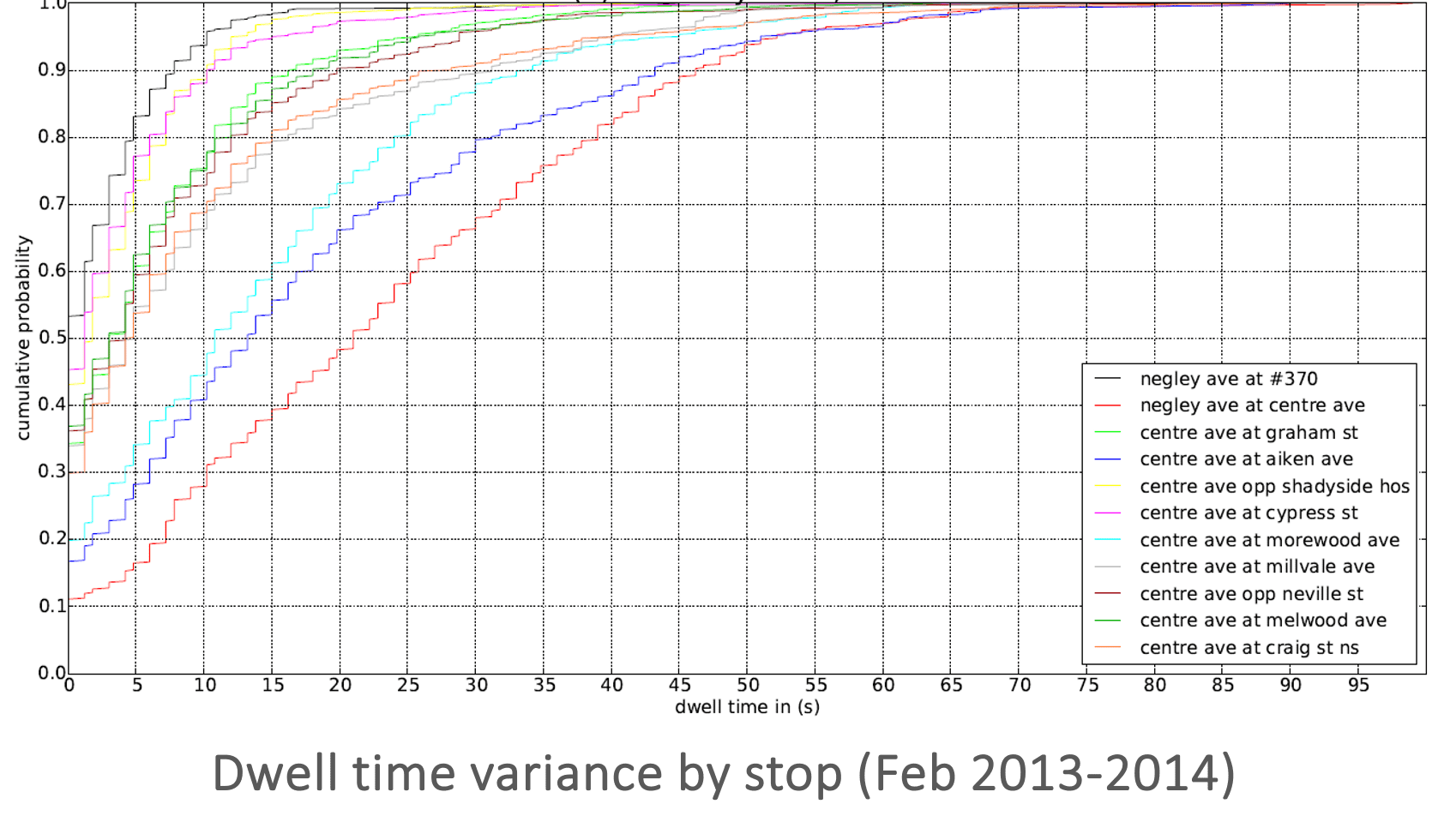
- Dwell times vary considerably by stop.
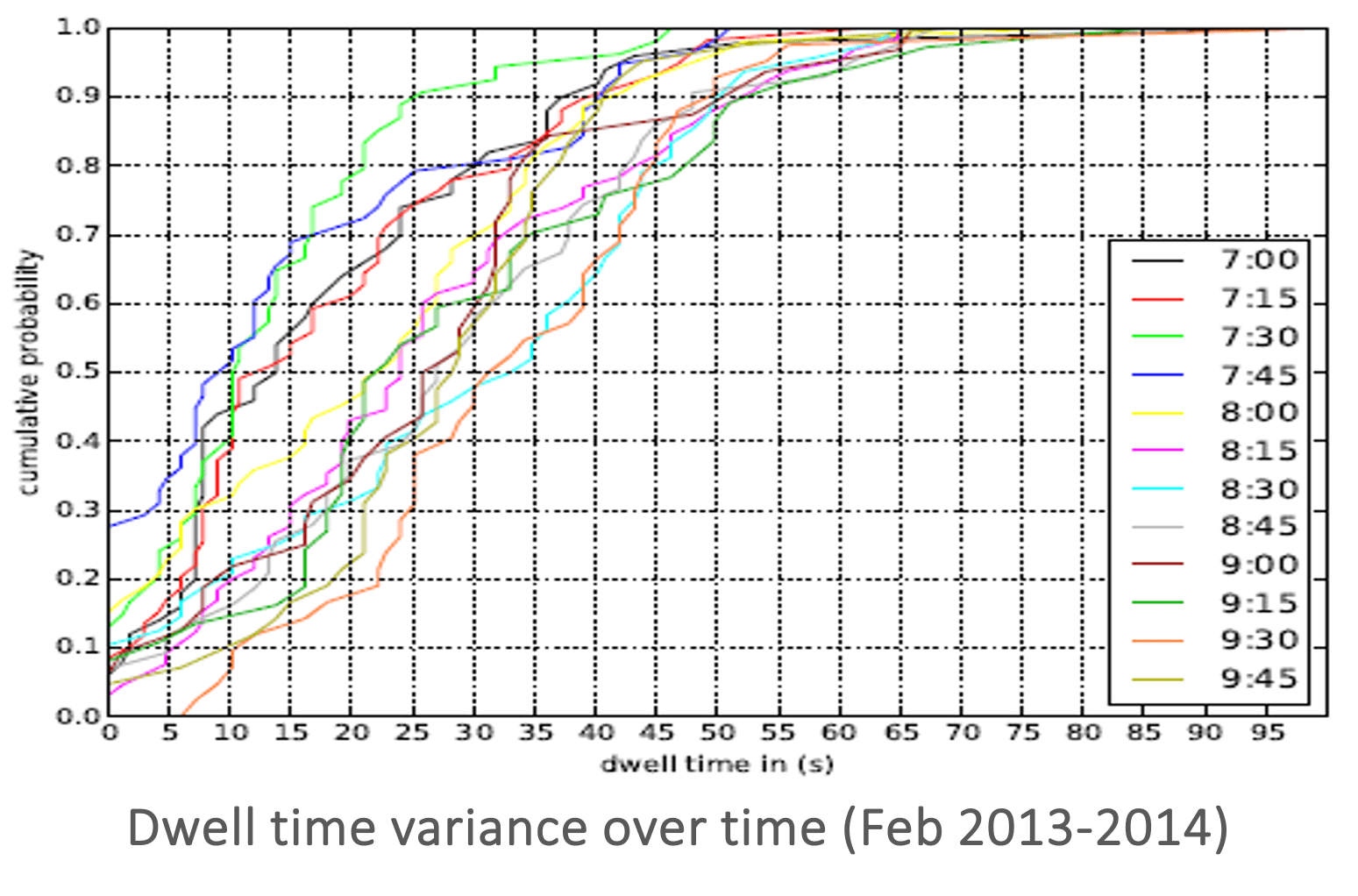
- Dwell times also vary considerably within peak periods.
Stage II: Generalized Predictive DT Models
Stage Overview
Goal:
- Probabilistic models of bus dwell times for each bus route and bus stop
- Highly stochastic behavior requires a technique that needs only a few data samples
Approach: Hierarchical, Bayes nets
Performance
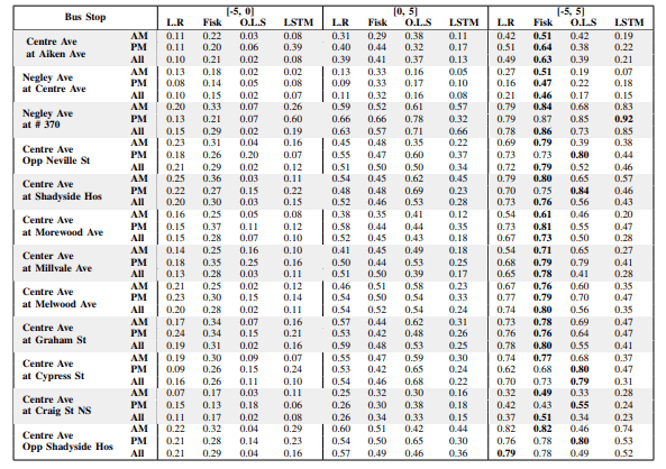
- Accurate predictions after just 20 data samples
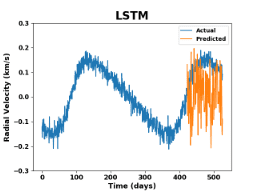
- Significantly outperforms standard linear regression techniques, online linear regression techniques, and deep learning
Stage-III: Improve Algorithmic Performance
Stage Overview
Goal:
- Improve the computational scalability of the dwell time prediction model
- The model needs to numerically approximate an 8-10 dimensional integral
- Computation needs ~ 7–250 seconds
- Existing model can’t be used in real-time
Approach:
- Identified a numerical integration algorithm used to analyze astronomy data
- Extended the approximation algorithm to real-time computation
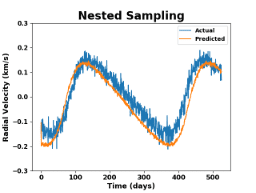
- Incorporated it into a Bayesian sequential learning framework
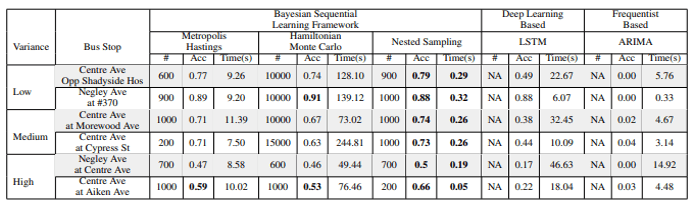
Performance:
- Average computational time reduced to 0.23 seconds without compromising accuracy
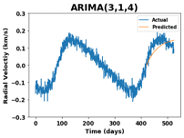
- Significantly outperforms other numerical integration algorithms (Metropolis-Hastings, Hamiltonian Monte Carlo)
Application: Grant Street Area Simulation
Existing Timing Plans